Basic manipulation of circuits
The goal of this notebook is to explore main possibilities and manipulation of quantum circuits offered by MPQP.
Instantiation and display the circuit
We first import QCircuit, the class representing quantum circuits.
[1]:
from mpqp import QCircuit
The first argument taken by the constructor of QCircuit is either the number of qubits, or a list of Instruction.
One can instanciate an empty circuit by only giving its number of qubits. The number of classical bits is automatically handled by the class, and thus is optional. We can also attach to a circuit a given label.
[2]:
circ1 = QCircuit(3)
circ2 = QCircuit(5, nb_cbits=2, label="Example")
Then, one can add at the end of the circuit an instruction or list of instructions. For that, we add the right imports.
[3]:
from mpqp.gates import *
from mpqp.measures import BasisMeasure
from mpqp import Barrier
[4]:
circ2.add(CNOT(2,3))
circ2.add([H(0), T(1), CNOT(0,1), S(4)])
As previously stated, we can also instantiate and initialize the circuit with a list of Instruction (gates or measurements).
[5]:
circ3 = QCircuit(
[
H(0),
X(1),
CNOT(1, 2),
Barrier(),
Y(2),
Z(0),
CZ(1, 0),
BasisMeasure([0, 1, 2], shots=1024),
]
)
We can then print the circuit directly as a string, or use pretty_print for more detailed information on the circuit.
[6]:
print(circ2)
┌───┐
q_0: ┤ H ├──■──
├───┤┌─┴─┐
q_1: ┤ T ├┤ X ├
└───┘└───┘
q_2: ──■───────
┌─┴─┐
q_3: ┤ X ├─────
├───┤
q_4: ┤ S ├─────
└───┘
c: 2/══════════
[7]:
circ3.pretty_print()
QCircuit : Size (Qubits, Cbits) = (3, 3), Nb instructions = 8
┌───┐ ░ ┌───┐ ┌─┐
q_0: ┤ H ├──────░─┤ Z ├─■─┤M├───
├───┤ ░ └───┘ │ └╥┘┌─┐
q_1: ┤ X ├──■───░───────■──╫─┤M├
└───┘┌─┴─┐ ░ ┌───┐┌─┐ ║ └╥┘
q_2: ─────┤ X ├─░─┤ Y ├┤M├─╫──╫─
└───┘ ░ └───┘└╥┘ ║ ║
c: 3/═══════════════════╩══╩══╩═
2 0 1
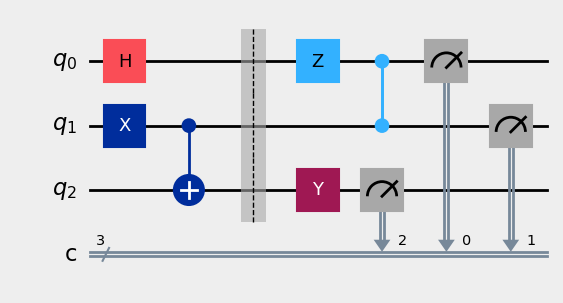
We can also use the method display to render the circuit in different formats. The default one uses matplotlib, but other options can be given in parameters (the same as the qiskit display function).
[8]:
circ3.display(warn=False)
[8]:
[9]:
circ3.display("latex")
[9]:
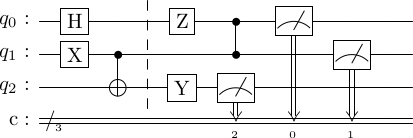
Retrieve circuit properties
One can also retrieve different properties of the circuit, including the depth, the size (quantum and classical bits), counting (specific) gates and retrieving the attached measurements.
[10]:
circ3.depth()
[10]:
4
[11]:
circ3.size()
[11]:
(3, 3)
[12]:
circ3.count_gates(X)
[12]:
1
[13]:
circ3.measurements
[13]:
[BasisMeasure([0, 1, 2])]
Combination of circuits
We also allow combinations of circuits.
[14]:
circ1 = QCircuit([H(0), S(1), CNOT(0,1)])
circ2 = QCircuit([X(0)])
print(circ1)
print('-------------')
print(circ2)
┌───┐
q_0: ┤ H ├──■──
├───┤┌─┴─┐
q_1: ┤ S ├┤ X ├
└───┘└───┘
-------------
┌───┐
q: ┤ X ├
└───┘
One can append a circuit to another, consisting in concatenating the circuit horizontally at the right of the first one. For more simplicity, the + realized the same operation. When the size does not match, we automatically adjust the size of the resulting circuit.
[15]:
appended = circ1 + circ2
print(appended)
┌───┐ ┌───┐
q_0: ┤ H ├──■──┤ X ├
├───┤┌─┴─┐└───┘
q_1: ┤ S ├┤ X ├─────
└───┘└───┘
One can also take the tensor product of two circuits using the method tensor, or the symbol @, which will concatenate the second circuit vertically under the first.
[16]:
tensored = circ1 @ circ2
print(tensored)
┌───┐
q_0: ┤ H ├──■──
├───┤┌─┴─┐
q_1: ┤ S ├┤ X ├
├───┤└───┘
q_2: ┤ X ├─────
└───┘
Translating the circuit
MPQP is a multi-platform quantum programming library and handles for the user the translation of circuits. We allow the user to use a function to export the circuit in different objects specific to each SDK using the method to_other_language.
[17]:
from mpqp import Language
circ3.to_other_language(Language.QISKIT)
[17]:
<qiskit.circuit.quantumcircuit.QuantumCircuit at 0x27bdbe8db50>
[18]:
circ3.to_other_language(Language.MY_QLM)
[18]:
Circuit(ops=[Op(gate='H', qbits=[0], type=0, cbits=None, formula=None, remap=None), Op(gate='X', qbits=[1], type=0, cbits=None, formula=None, remap=None), Op(gate='CNOT', qbits=[1, 2], type=0, cbits=None, formula=None, remap=None), Op(gate='Y', qbits=[2], type=0, cbits=None, formula=None, remap=None), Op(gate='Z', qbits=[0], type=0, cbits=None, formula=None, remap=None), Op(gate='CSIGN', qbits=[1, 0], type=0, cbits=None, formula=None, remap=None)], name=None, gateDic={'X': GateDefinition(name='X', arity=1, matrix=Matrix(nRows=2, nCols=2, data=[ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0)]), is_ctrl=False, is_dag=None, is_trans=None, is_conj=None, subgate=None, syntax=GSyntax(name='X', parameters=[]), nbctrls=None, circuit_implementation=None), 'Y': GateDefinition(name='Y', arity=1, matrix=Matrix(nRows=2, nCols=2, data=[ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=-0.0, im=-1.0), ComplexNumber(re=0.0, im=1.0), ComplexNumber(re=0.0, im=0.0)]), is_ctrl=False, is_dag=None, is_trans=None, is_conj=None, subgate=None, syntax=GSyntax(name='Y', parameters=[]), nbctrls=None, circuit_implementation=None), 'Z': GateDefinition(name='Z', arity=1, matrix=Matrix(nRows=2, nCols=2, data=[ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=-1.0, im=0.0)]), is_ctrl=False, is_dag=None, is_trans=None, is_conj=None, subgate=None, syntax=GSyntax(name='Z', parameters=[]), nbctrls=None, circuit_implementation=None), 'H': GateDefinition(name='H', arity=1, matrix=Matrix(nRows=2, nCols=2, data=[ComplexNumber(re=0.7071067811865475, im=0.0), ComplexNumber(re=0.7071067811865475, im=0.0), ComplexNumber(re=0.7071067811865475, im=0.0), ComplexNumber(re=-0.7071067811865475, im=0.0)]), is_ctrl=False, is_dag=None, is_trans=None, is_conj=None, subgate=None, syntax=GSyntax(name='H', parameters=[]), nbctrls=None, circuit_implementation=None), 'CNOT': GateDefinition(name='CNOT', arity=2, matrix=Matrix(nRows=4, nCols=4, data=[ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0)]), is_ctrl=True, is_dag=None, is_trans=None, is_conj=None, subgate='X', syntax=GSyntax(name='CNOT', parameters=[]), nbctrls=1, circuit_implementation=None), 'CSIGN': GateDefinition(name='CSIGN', arity=2, matrix=Matrix(nRows=4, nCols=4, data=[ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=-1.0, im=0.0)]), is_ctrl=True, is_dag=None, is_trans=None, is_conj=None, subgate='Z', syntax=GSyntax(name='CSIGN', parameters=[]), nbctrls=1, circuit_implementation=None), 'ISWAP': GateDefinition(name='ISWAP', arity=2, matrix=Matrix(nRows=4, nCols=4, data=[ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=1.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=1.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0)]), is_ctrl=False, is_dag=None, is_trans=None, is_conj=None, subgate=None, syntax=GSyntax(name='ISWAP', parameters=[]), nbctrls=None, circuit_implementation=None), 'SQRTSWAP': GateDefinition(name='SQRTSWAP', arity=2, matrix=Matrix(nRows=4, nCols=4, data=[ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.5, im=0.5), ComplexNumber(re=0.5, im=-0.5), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.5, im=-0.5), ComplexNumber(re=0.5, im=0.5), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0)]), is_ctrl=False, is_dag=None, is_trans=None, is_conj=None, subgate=None, syntax=GSyntax(name='SQRTSWAP', parameters=[]), nbctrls=None, circuit_implementation=None), 'I': GateDefinition(name='I', arity=1, matrix=Matrix(nRows=2, nCols=2, data=[ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0)]), is_ctrl=False, is_dag=None, is_trans=None, is_conj=None, subgate=None, syntax=GSyntax(name='I', parameters=[]), nbctrls=None, circuit_implementation=None), 'SWAP': GateDefinition(name='SWAP', arity=2, matrix=Matrix(nRows=4, nCols=4, data=[ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0)]), is_ctrl=False, is_dag=None, is_trans=None, is_conj=None, subgate=None, syntax=GSyntax(name='SWAP', parameters=[]), nbctrls=None, circuit_implementation=None), 'CCNOT': GateDefinition(name='CCNOT', arity=3, matrix=Matrix(nRows=8, nCols=8, data=[ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0)]), is_ctrl=True, is_dag=None, is_trans=None, is_conj=None, subgate='CNOT', syntax=GSyntax(name='CCNOT', parameters=[]), nbctrls=1, circuit_implementation=None), 'S': GateDefinition(name='S', arity=1, matrix=Matrix(nRows=2, nCols=2, data=[ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=1.0)]), is_ctrl=False, is_dag=None, is_trans=None, is_conj=None, subgate=None, syntax=GSyntax(name='S', parameters=[]), nbctrls=None, circuit_implementation=None), 'T': GateDefinition(name='T', arity=1, matrix=Matrix(nRows=2, nCols=2, data=[ComplexNumber(re=1.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.0, im=0.0), ComplexNumber(re=0.7071067811865476, im=0.7071067811865476)]), is_ctrl=False, is_dag=None, is_trans=None, is_conj=None, subgate=None, syntax=GSyntax(name='T', parameters=[]), nbctrls=None, circuit_implementation=None)}, nbqbits=3, nbcbits=0, _gate_set=GateSet(gate_signatures={'X': GateSignature(name='X', parameters=[], arity=1, nb_args=0, arg_types=[], arity_generator=None, matrix_generator=<cyfunction gen_x at 0x0000027BDC1E93C0>, circuit_generator=None), 'Y': GateSignature(name='Y', parameters=[], arity=1, nb_args=0, arg_types=[], arity_generator=None, matrix_generator=<cyfunction gen_y at 0x0000027BDC1E9490>, circuit_generator=None), 'Z': GateSignature(name='Z', parameters=[], arity=1, nb_args=0, arg_types=[], arity_generator=None, matrix_generator=<cyfunction gen_z at 0x0000027BDC1E9560>, circuit_generator=None), 'H': GateSignature(name='H', parameters=[], arity=1, nb_args=0, arg_types=[], arity_generator=None, matrix_generator=<cyfunction gen_h at 0x0000027BDC1E92F0>, circuit_generator=None), 'CNOT': GateSignature(name='CNOT', parameters=[], arity=2, nb_args=0, arg_types=[], arity_generator=None, matrix_generator=<cyfunction gen_cnot at 0x0000027BDC1E98A0>, circuit_generator=None), 'CSIGN': GateSignature(name='CSIGN', parameters=[], arity=2, nb_args=0, arg_types=[], arity_generator=None, matrix_generator=<cyfunction gen_csign at 0x0000027BDC1E9970>, circuit_generator=None), 'ISWAP': GateSignature(name='ISWAP', parameters=[], arity=2, nb_args=0, arg_types=[], arity_generator=None, matrix_generator=<cyfunction gen_iswap at 0x0000027BDC1E9BE0>, circuit_generator=None), 'SQRTSWAP': GateSignature(name='SQRTSWAP', parameters=[], arity=2, nb_args=0, arg_types=[], arity_generator=None, matrix_generator=<cyfunction gen_sqrtswap at 0x0000027BDC1E9B10>, circuit_generator=None), 'I': GateSignature(name='I', parameters=[], arity=1, nb_args=0, arg_types=[], arity_generator=None, matrix_generator=<cyfunction gen_i at 0x0000027BDC1E9630>, circuit_generator=None), 'SWAP': GateSignature(name='SWAP', parameters=[], arity=2, nb_args=0, arg_types=[], arity_generator=None, matrix_generator=<cyfunction gen_swap at 0x0000027BDC1E9A40>, circuit_generator=None), 'CCNOT': GateSignature(name='CCNOT', parameters=[], arity=3, nb_args=0, arg_types=[], arity_generator=None, matrix_generator=<cyfunction gen_ccnot at 0x0000027BDC1E9CB0>, circuit_generator=None), 'S': GateSignature(name='S', parameters=[], arity=1, nb_args=0, arg_types=[], arity_generator=None, matrix_generator=<cyfunction gen_s at 0x0000027BDC1E9700>, circuit_generator=None), 'T': GateSignature(name='T', parameters=[], arity=1, nb_args=0, arg_types=[], arity_generator=None, matrix_generator=<cyfunction gen_t at 0x0000027BDC1E97D0>, circuit_generator=None), 'PH': GateSignature(name='PH', parameters=[1], arity=1, nb_args=1, arg_types=[<class 'float'>], arity_generator=None, matrix_generator=<cyfunction gen_ph at 0x0000027BDC1E8E10>, circuit_generator=None), 'RZ': GateSignature(name='RZ', parameters=[1], arity=1, nb_args=1, arg_types=[<class 'float'>], arity_generator=None, matrix_generator=<cyfunction gen_rz at 0x0000027BDC1E8EE0>, circuit_generator=None), 'RX': GateSignature(name='RX', parameters=[1], arity=1, nb_args=1, arg_types=[<class 'float'>], arity_generator=None, matrix_generator=<cyfunction gen_rx at 0x0000027BDC1E9080>, circuit_generator=None), 'RY': GateSignature(name='RY', parameters=[1], arity=1, nb_args=1, arg_types=[<class 'float'>], arity_generator=None, matrix_generator=<cyfunction gen_ry at 0x0000027BDC1E8FB0>, circuit_generator=None), 'U': AbstractGate(name='U', parameters=[1, 1, 1], arity=1, nb_args=3, arg_types=[<class 'float'>, <class 'float'>, <class 'float'>], arity_generator=None, matrix_generator=<function gen_U at 0x0000027BDC173420>, circuit_generator=None, dag_func=None), 'U1': AbstractGate(name='U1', parameters=[1], arity=1, nb_args=1, arg_types=[<class 'float'>], arity_generator=None, matrix_generator=<function gen_u1 at 0x0000027BDC559300>, circuit_generator=None, dag_func=None), 'U2': AbstractGate(name='U2', parameters=[1, 1], arity=1, nb_args=2, arg_types=[<class 'float'>, <class 'float'>], arity_generator=None, matrix_generator=<function gen_u2 at 0x0000027BDC5593A0>, circuit_generator=None, dag_func=None), 'U3': AbstractGate(name='U3', parameters=[1, 1, 1], arity=1, nb_args=3, arg_types=[<class 'float'>, <class 'float'>, <class 'float'>], arity_generator=None, matrix_generator=<function gen_U at 0x0000027BDC173420>, circuit_generator=None, dag_func=None)}), has_matrices=True, var_dic={}, qregs=[], ancilla_map=None, _serialized_gate_set=b"\x80\x04\x95?\x06\x00\x00\x00\x00\x00\x00\x8c\x11qat.core.gate_set\x94\x8c\x07GateSet\x94\x93\x94)\x81\x94}\x94\x8c\x0fgate_signatures\x94}\x94(\x8c\x01X\x94h\x00\x8c\rGateSignature\x94\x93\x94)\x81\x94}\x94(\x8c\x04name\x94h\x07\x8c\nparameters\x94]\x94\x8c\x05arity\x94K\x01\x8c\x07nb_args\x94K\x00\x8c\targ_types\x94]\x94\x8c\x0farity_generator\x94N\x8c\x10matrix_generator\x94\x8c$qat.core.circuit_builder.matrix_util\x94\x8c\x05gen_x\x94\x93\x94\x8c\x11circuit_generator\x94Nub\x8c\x01Y\x94h\t)\x81\x94}\x94(h\x0ch\x19h\r]\x94h\x0fK\x01h\x10K\x00h\x11]\x94h\x13Nh\x14h\x15\x8c\x05gen_y\x94\x93\x94h\x18Nub\x8c\x01Z\x94h\t)\x81\x94}\x94(h\x0ch h\r]\x94h\x0fK\x01h\x10K\x00h\x11]\x94h\x13Nh\x14h\x15\x8c\x05gen_z\x94\x93\x94h\x18Nub\x8c\x01H\x94h\t)\x81\x94}\x94(h\x0ch'h\r]\x94h\x0fK\x01h\x10K\x00h\x11]\x94h\x13Nh\x14h\x15\x8c\x05gen_h\x94\x93\x94h\x18Nub\x8c\x04CNOT\x94h\t)\x81\x94}\x94(h\x0ch.h\r]\x94h\x0fK\x02h\x10K\x00h\x11]\x94h\x13Nh\x14h\x15\x8c\x08gen_cnot\x94\x93\x94h\x18Nub\x8c\x05CSIGN\x94h\t)\x81\x94}\x94(h\x0ch5h\r]\x94h\x0fK\x02h\x10K\x00h\x11]\x94h\x13Nh\x14h\x15\x8c\tgen_csign\x94\x93\x94h\x18Nub\x8c\x05ISWAP\x94h\t)\x81\x94}\x94(h\x0ch<h\r]\x94h\x0fK\x02h\x10K\x00h\x11]\x94h\x13Nh\x14h\x15\x8c\tgen_iswap\x94\x93\x94h\x18Nub\x8c\x08SQRTSWAP\x94h\t)\x81\x94}\x94(h\x0chCh\r]\x94h\x0fK\x02h\x10K\x00h\x11]\x94h\x13Nh\x14h\x15\x8c\x0cgen_sqrtswap\x94\x93\x94h\x18Nub\x8c\x01I\x94h\t)\x81\x94}\x94(h\x0chJh\r]\x94h\x0fK\x01h\x10K\x00h\x11]\x94h\x13Nh\x14h\x15\x8c\x05gen_i\x94\x93\x94h\x18Nub\x8c\x04SWAP\x94h\t)\x81\x94}\x94(h\x0chQh\r]\x94h\x0fK\x02h\x10K\x00h\x11]\x94h\x13Nh\x14h\x15\x8c\x08gen_swap\x94\x93\x94h\x18Nub\x8c\x05CCNOT\x94h\t)\x81\x94}\x94(h\x0chXh\r]\x94h\x0fK\x03h\x10K\x00h\x11]\x94h\x13Nh\x14h\x15\x8c\tgen_ccnot\x94\x93\x94h\x18Nub\x8c\x01S\x94h\t)\x81\x94}\x94(h\x0ch_h\r]\x94h\x0fK\x01h\x10K\x00h\x11]\x94h\x13Nh\x14h\x15\x8c\x05gen_s\x94\x93\x94h\x18Nub\x8c\x01T\x94h\t)\x81\x94}\x94(h\x0chfh\r]\x94h\x0fK\x01h\x10K\x00h\x11]\x94h\x13Nh\x14h\x15\x8c\x05gen_t\x94\x93\x94h\x18Nub\x8c\x02PH\x94h\t)\x81\x94}\x94(h\x0chmh\r]\x94K\x01ah\x0fK\x01h\x10K\x01h\x11]\x94\x8c\ndill._dill\x94\x8c\n_load_type\x94\x93\x94\x8c\x05float\x94\x85\x94R\x94ah\x13Nh\x14h\x15\x8c\x06gen_ph\x94\x93\x94h\x18Nub\x8c\x02RZ\x94h\t)\x81\x94}\x94(h\x0chzh\r]\x94K\x01ah\x0fK\x01h\x10K\x01h\x11]\x94hwah\x13Nh\x14h\x15\x8c\x06gen_rz\x94\x93\x94h\x18Nub\x8c\x02RX\x94h\t)\x81\x94}\x94(h\x0ch\x81h\r]\x94K\x01ah\x0fK\x01h\x10K\x01h\x11]\x94hwah\x13Nh\x14h\x15\x8c\x06gen_rx\x94\x93\x94h\x18Nub\x8c\x02RY\x94h\t)\x81\x94}\x94(h\x0ch\x88h\r]\x94K\x01ah\x0fK\x01h\x10K\x01h\x11]\x94hwah\x13Nh\x14h\x15\x8c\x06gen_ry\x94\x93\x94h\x18Nub\x8c\x01U\x94\x8c\x14qat.lang.AQASM.gates\x94\x8c\x0cAbstractGate\x94\x93\x94)\x81\x94}\x94(h\x0ch\x8fh\r]\x94(K\x01K\x01K\x01eh\x0fK\x01h\x10K\x03h\x11]\x94(hwhwhweh\x13Nh\x14\x8c qat.interop.openqasm.qasm_parser\x94\x8c\x05gen_U\x94\x93\x94h\x18N\x8c\x08dag_func\x94Nub\x8c\x02U1\x94h\x92)\x81\x94}\x94(h\x0ch\x9bh\r]\x94K\x01ah\x0fK\x01h\x10K\x01h\x11]\x94hwah\x13Nh\x14h\x97\x8c\x06gen_u1\x94\x93\x94h\x18Nh\x9aNub\x8c\x02U2\x94h\x92)\x81\x94}\x94(h\x0ch\xa2h\r]\x94(K\x01K\x01eh\x0fK\x01h\x10K\x02h\x11]\x94(hwhweh\x13Nh\x14h\x97\x8c\x06gen_u2\x94\x93\x94h\x18Nh\x9aNub\x8c\x02U3\x94h\x92)\x81\x94}\x94(h\x0ch\xa9h\r]\x94(K\x01K\x01K\x01eh\x0fK\x01h\x10K\x03h\x11]\x94(hwhwhweh\x13Nh\x14h\x99h\x18Nh\x9aNubusb.")
[19]:
circ3.to_other_language(Language.BRAKET, translation_warning=False)
[19]:
Circuit('instructions': [Instruction('operator': H('qubit_count': 1), 'target': QubitSet([Qubit(0)]), 'control': QubitSet([]), 'control_state': (), 'power': 1), Instruction('operator': X('qubit_count': 1), 'target': QubitSet([Qubit(1)]), 'control': QubitSet([]), 'control_state': (), 'power': 1), Instruction('operator': CNot('qubit_count': 2), 'target': QubitSet([Qubit(1), Qubit(2)]), 'control': QubitSet([]), 'control_state': (), 'power': 1), Instruction('operator': Y('qubit_count': 1), 'target': QubitSet([Qubit(2)]), 'control': QubitSet([]), 'control_state': (), 'power': 1), Instruction('operator': Z('qubit_count': 1), 'target': QubitSet([Qubit(0)]), 'control': QubitSet([]), 'control_state': (), 'power': 1), Instruction('operator': CZ('qubit_count': 2), 'target': QubitSet([Qubit(1), Qubit(0)]), 'control': QubitSet([]), 'control_state': (), 'power': 1)])
[20]:
circ3.to_other_language(Language.CIRQ)
[20]:
q_0: ───I───H───Z───@───M('')───
│ │
q_1: ───I───X───@───@───M───────
│ │
q_2: ───I───────X───Y───M───────Since we use OpenQASM as a common standard for circuit translation, we also provide for the user a way to retrive the code of the circuit in OpenQASM 2.0 and 3.0.
[21]:
print(circ3.to_other_language(Language.QASM2))
OPENQASM 2.0;
include "qelib1.inc";
qreg q[3];
creg c[3];
h q[0];
x q[1];
cx q[1],q[2];
barrier q[0],q[1],q[2];
y q[2];
z q[0];
cz q[1],q[0];
measure q[0] -> c[0];
measure q[1] -> c[1];
measure q[2] -> c[2];
[22]:
print(circ3.to_other_language(Language.QASM3))
OPENQASM 3.0;
include "stdgates.inc";
qubit[3] q;
bit[3] c;
h q[0];
x q[1];
cx q[1],q[2];
barrier q[0],q[1],q[2];
y q[2];
z q[0];
cz q[1],q[0];
c[0] = measure q[0];
c[1] = measure q[1];
c[2] = measure q[2];
Parametrized circuit
We allow the use and manipulation of symbolic variable to parametrize gates.
We first declare symbolic variables using symbols (yes, we indeed use sympy!).
[23]:
from sympy import symbols
theta, k = symbols("θ k")
We can then use these variables to instantiate and add ParametrizedGate to the circuit.
[24]:
param_circ = QCircuit(
[Rx(theta, 0), CNOT(1,2), X(2), Rk(k,1), H(0), CRk(k, 0, 2),
BasisMeasure(list(range(3)), shots=1000)]
)
One can observe, in the print below, that 3 gates depend on variables.
[25]:
print(param_circ)
┌───────┐ ┌───┐ ┌─┐
q_0: ┤ Rx(θ) ├───────┤ H ├─────────■────────────────────┤M├───
└───────┘┌──────┴───┴───────┐ │ ┌─┐└╥┘
q_1: ────■────┤ P(2**(1 - k)*pi) ├─┼─────────────────┤M├─╫────
┌─┴─┐ └──────┬───┬───────┘ │P(2**(1 - k)*pi) └╥┘ ║ ┌─┐
q_2: ──┤ X ├─────────┤ X ├─────────■──────────────────╫──╫─┤M├
└───┘ └───┘ ║ ║ └╥┘
c: 3/═════════════════════════════════════════════════╩══╩══╩═
1 0 2
If we want to attribute values to the parameters, one can use the method subs as follows. This will return a new circuit with the gates’ parameters given in subs. One can also choose to substitute symbolic variable with real and complex numbers when call the run function (at execution).
[26]:
import numpy as np
print(param_circ.subs({theta: np.pi/3, k:2}))
┌─────────┐ ┌───┐ ┌─┐
q_0: ┤ Rx(π/3) ├──┤ H ├────■──────────┤M├───
└─────────┘┌─┴───┴──┐ │ ┌─┐└╥┘
q_1: ─────■─────┤ P(π/2) ├─┼───────┤M├─╫────
┌─┴─┐ └─┬───┬──┘ │P(π/2) └╥┘ ║ ┌─┐
q_2: ───┤ X ├─────┤ X ├────■────────╫──╫─┤M├
└───┘ └───┘ ║ ║ └╥┘
c: 3/═══════════════════════════════╩══╩══╩═
1 0 2
One can also retrieve the set of variables in the circuit by calling the variables() method.
[27]:
param_circ.variables()
[27]:
{k, θ}